Find the probability of z occurring in the indicated region – Delving into the realm of probability theory, we embark on an exploration of finding the probability of Z occurring within a specified region. This concept holds immense significance in statistical analysis and forms the cornerstone of various real-world applications.

By transforming a random variable into a standard normal variable (Z-score), we unlock the power to calculate the likelihood of Z falling within a given interval. This transformation allows us to leverage the well-defined properties of the standard normal distribution, providing a standardized framework for probability calculations.

Probability Theory

Probability theory is the branch of mathematics that deals with the likelihood of events occurring. It provides a framework for quantifying the uncertainty associated with random events and making predictions about future outcomes.

Key concepts in probability theory include:

• Sample space: The set of all possible outcomes of an experiment.
• Event: A subset of the sample space.
• Probability: A numerical measure of the likelihood of an event occurring.

Standard Normal Distribution

The standard normal distribution, also known as the Gaussian distribution or bell curve, is a continuous probability distribution that is defined by two parameters: mean (μ) and standard deviation (σ).

The probability density function (PDF) of the standard normal distribution is given by:

f(z) = (1 / √(2π))

e^(-z^2 / 2)

where z is the standardized value of a random variable X, defined as:

z = (X

μ) / σ

The cumulative distribution function (CDF) of the standard normal distribution is given by:

F(z) = P(X ≤ z) = (1 / √(2π))

∫^z_-∞e^(-t^2 / 2) dt

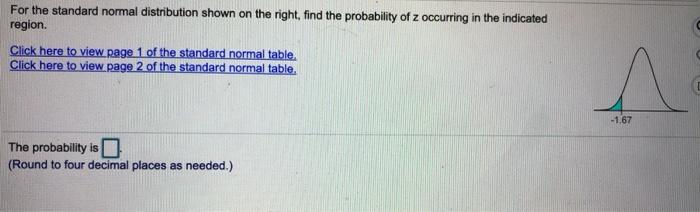
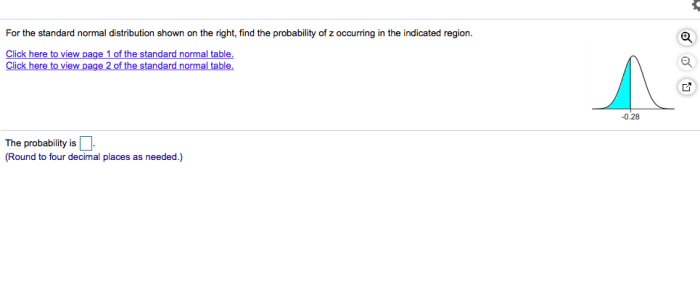
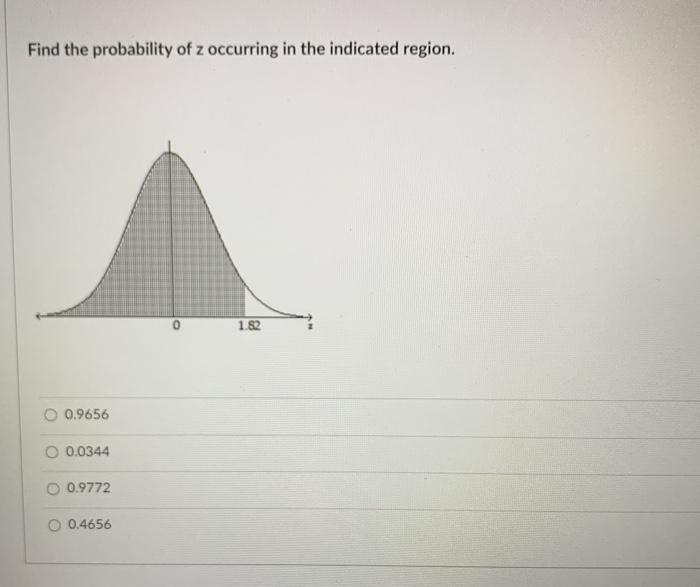
Finding Probabilities for Z

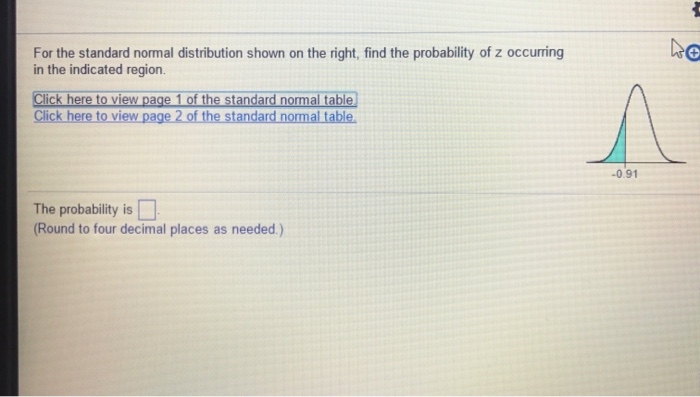
To find the probability of Z occurring in a given region, we use the CDF of the standard normal distribution. The probability of Z being between z ₁and z ₂is given by:

P(z₁≤ Z ≤ z ₂) = F(z ₂)

F(z₁)

Applications

Finding probabilities for Z has numerous applications in real-world scenarios, including:

• Hypothesis testing: Determining the likelihood of obtaining a sample result if the null hypothesis is true.
• Confidence intervals: Estimating the range within which a population parameter is likely to fall.
• Quality control: Assessing the probability of a product meeting certain specifications.
• Financial modeling: Predicting the likelihood of financial events, such as stock prices or bond yields.

Quick FAQs: Find The Probability Of Z Occurring In The Indicated Region

What is the significance of finding probabilities for Z?

Finding probabilities for Z allows us to quantify the likelihood of events occurring within a specified range, providing a basis for statistical inference and decision-making.

How do we transform a random variable into a standard normal variable?

To transform a random variable into a standard normal variable, we subtract the mean and divide by the standard deviation, resulting in a Z-score that follows the standard normal distribution.